What are inequalities?
Instead of having an equation with an = sign, it can sometimes have signs like > and <. This means that the answer will be a range of values.
Steps
Right hand side (RHS)
Left hand side (LHS)
1. Make the RHS 0 by shifting all the terms to the LHS.
2. Factorise the LHS.
3. Draw a graph (a rough sketch)
4. Determine the values required from a graph.
EXAMPLE
x2 + 2x – 15 > 0
(x + 5)(x – 3) > 0
x = -5 / x = 3
You have to solve the equation as if it is = 0 instead of an inequality so that you can find the x-intercepts. This will help you with step 3 of “draw a graph”.
How to sketch the graph
The coefficient of x2 will tell you if the graph will have a maximum or minimum.
- Positive coefficient = minimum
- Negative coefficient = maximum

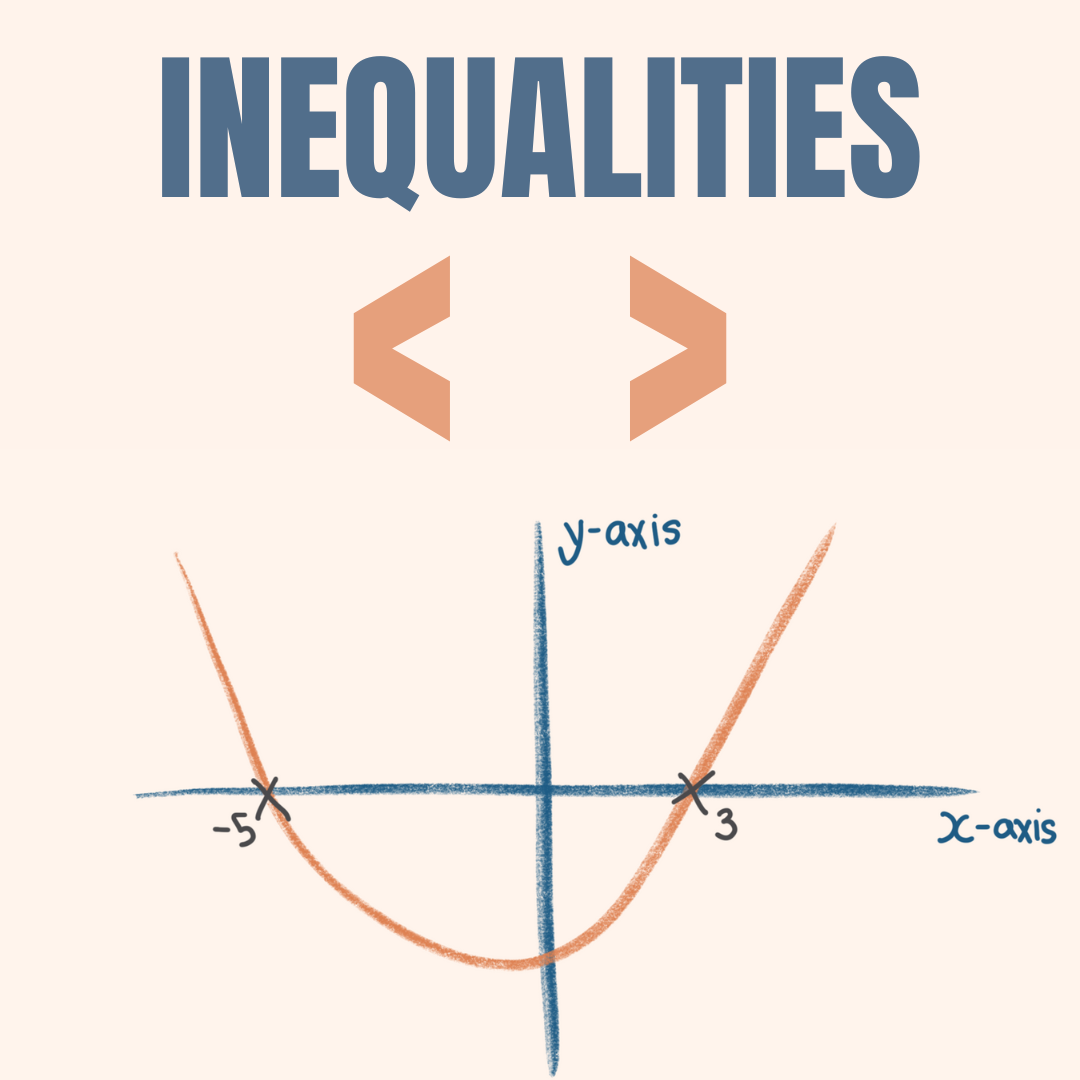
In this example, the coefficient is positive. Next, we can sketch the graph so that it cuts the x-axis at the points we found (-5 and 3).

When we shift all the terms to the LHS, it shows us that we need to find the part of the graph that is > 0. Therefore, we can highlight the part of the graph that is above 0.

This shows us that anything left of x = -5 is above 0 and anything right of 3 is also above 0.
Our final answer is:
x < -5, x > 3

Leave a Reply