So, the quadratic equation is an equation where the highest power of x is 2 (i.e., x2), but we can write it in different ways. For example:
- Standard form: y=ax^2+bx+c
- Factored form: y=a(x-r_1)(x-r_2)
- Vertex form: y=a(x-h)^2+k
All of these are still the quadratic equation – the terms are just arranged differently, sometimes grouped together, or factored. The highest power of the equation is still x2
For the factored form, you don’t directly see x2, but if you multiply it out, you will see the power is x2.
The letters in these formulas a, b, c, r1, r2, h and k are just letters to represent any number. E.g. if a = 1, b =2, c = 1 then y=x^2+2x+1.
It doesn’t matter if the quadratic equation is arranged differently than this, eg. x^2+2x=y-1 is still a quadratic equation. It’s just that the 3 forms of arranging above is more useful for telling us things about the equation or graph.
Standard form
y=ax^2+bx+c
We usually write quadratic equations in the standard form because we can use the values of a, b, and c to solve the equation and find x, using the quadratic formula. However, if the equation is not in this form, we first have to rearrange it in this way so that we use the correct values of a, b and c when substituting it into the equation.
I will make a separate notes about the quadratic formula
On the graph, the values of a, b and c all have different effects on the shape of the graph:
- ‘a’ controls the “stretch” of the graph
- ‘b’ controls the horizontal position
- ‘c’ controls the vertical position (intercept)
The intercept is the point where the graph crosses the y-axis. So, if ‘c’ is 5, it tells us that the graph crosses the y-axis at the y-value 5. Or at the coordinates (0, 5).
The x-coordinate of a y-intercept will always be 0 because the y-axis is the vertical line that goes through the 0 x-value.



Factored form
y=a(x-r_1)(x-r2)
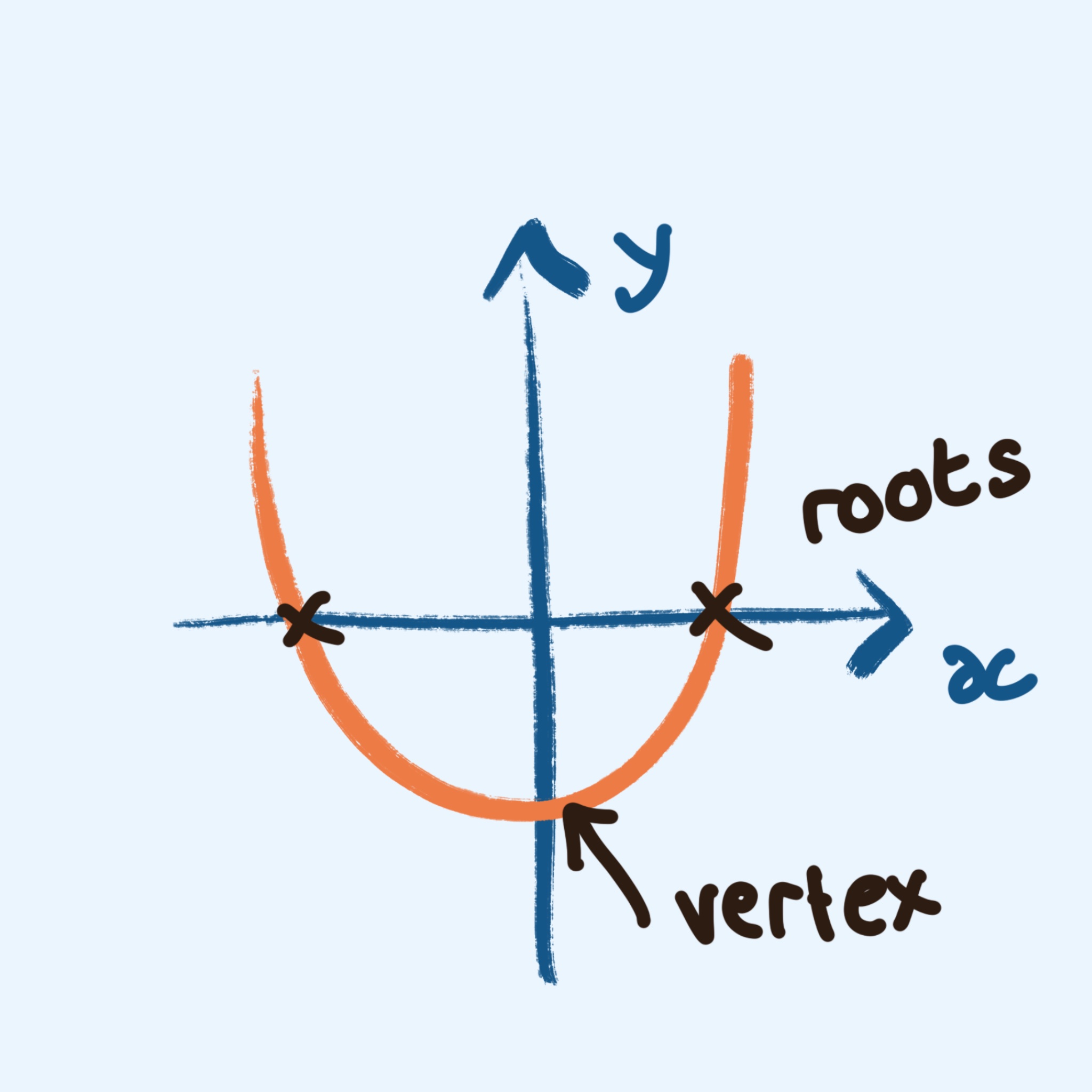
When you have a quadratic equation in the standard form, you can factorize it and then it will be in this form. This is another useful form for solving the equation. r1 and r2 give the roots of this equation. Roots are similar to the solutions of an equation:
- Solutions: Value(s) of x for a given y
- Roots: Value(s) of x when y = 0
On a graph, the roots are the points where the graph crosses the x-axis. You can either have 1 root, 2 roots, or no roots.

Vertex form
y=a(x-h)^2+k
Vertex is just a fancy math word to say “point” or “corner.” In terms of a quadratic equation, it is the top or bottom of the graph. When we write the equation in vertex form, it tells us where this “vertex” (top or bottom) is. The vertex is at the coordinate (h, k). So, h represents the x-coordinate of the point and k represents the y coordinate of the point.

So, in this case, the vertex is at (1, 1).
I’ll make specific notes about how to get from standard form to vertex form.

Leave a Reply